Methylation clocks have found their way into the community of aging research as a way to test anti-aging interventions without having to wait for mortality statistics. But methylation clocks are only useful for this purpose if aging is an epigenetic program, and most aging researchers still resist this paradigm. Just this year, some researchers have noticed this tension, and they have proposed that the methylation changes measured by epigenetic clocks are random drift, not under the body’s control. Below, I show why they are wrong about this, and why it may not even be possible to build an epigenetic clock based on unprogrammed drift.

---

Beginning in 2013, I took an early interest in methylation clocks because of the intrinsic link to programmed aging. It had became clear that gene expression was a powerful way to understand growth, development, and metabolism. Every cell in the body has the same genes, and these do not change over a lifetime. It is switching genes on and off in particular places and particular times that is responsible for all the essential processes of life.

Thus the default assumption is that gene expression = epigenetics is a tightly-controlled process. Genes are turned on when and where they are needed, and turned off otherwise. It was natural to think that the timing of gene expression to implement growth and development continued to implement an aging program later in life.

So, when Steve Horvath taught us that genes are turned on and off over a lifetime with the regularity of clockwork, I was enthusiastic about potential of the technology to evaluate anti-aging interventions. Not only that, I interpreted the regularity of gene expression changes with age as evidence for an aging program, and I said so.

The Horvath clocks were useful, and have been adopted. Some people were aware that the technology itself was a contradiction to their theoretical belief that aging is not (“cannot be”) under the body’s control. This tension between theory and practice has been simmering for 10 years, and just this year a proposed reconciliation has emerged: Three papers on stochastic methylation changes have been published in 2024. Their thesis is that methylation clocks are measuring loss of focus in the methylation pattern, rather than a directed process. “Dysregulation”, “stochastic change”, and “epigenetic entropy” are other names for the same idea.

My view is that these articles are ideologically motivated, and unconvincing. Yes, some of the changes in methylation that occur with age seem to be random and undirected. But the Horvath clocks were built on methylation sites that change most reliably and consistently over a lifetime. Sites that change randomly are less useful, and are left out of the algorithms. We have every reason to believe that their directed change with age is under the body’s control. 

I have written previously that there are two possibilities for the purpose of directed methylation changes over time. Type 1 changes are destroying the body, tending gradually toward programmed death. Inflammation, autoimmunity, and apoptosis are dialed up, while repair and quenching of ROS are dialed down. Type 2 changes are the opposite: the body perceives that it is in trouble and turns on repair programs. Type 2 changes are part of an ancient defense program, not explicitly timed to age, but reliably timed to the extent that the accumulation of damage (to which they respond) is reliably timed. 

Distinguishing Type 1 from Type 2 methylation changes remains a major challenge. Both are occurring simultaneously, and they are difficult to disentangle. But if we wish to use methylation clocks to measure the anti-aging benefits of an intervention, Type 1 and Type 2 should be counted in opposite directions. “Younger” according to Type 1 means less self-destruction, and this is good. “Younger” according to Type 2 means less repair, and this is bad. There is the danger that an intervention might interfere with the body’s repair, probably shortening life expectancy, but if our methylation clock includes Type 2 sites, the intervention might be scored as beneficial.

 

Stochastic clocks

Three research articles have been published this year promoting the idea that epigenetic clocks are based on methylation changes with age that are primarily stochastic. In other words, they are dysregulation, loss of information. My purpose in this column is to expose the fallacies in their methods. I believe that the way sites are selected for the clocks strongly selects for directed, non-random changes.

Entropic theories of aging have been discredited since the 19th century

Len Hayflick was a reigning sage of the aging biology community, and the most prominent proponent today of the theory that aging reflects an inevitable accumulation of entropy. Entropic theories of aging have never been coherent, but they are nevertheless experiencing a resurgence in recent years, primarily because neo-Darwinist theories of aging are all failing. I find this ironic, because the neo-Darwinist theories arose precisely because scientists realized that the Second Law of Thermodynamics does not apply to living systems. 

There is no necessity for entropy of living things to increase, because living things are constantly taking in low-entropy food and dumping high-entropy waste products into the environment. In fact, living things accumulate information as they grow. All of life is an end run around the Second Law of Thermodynamics. Therefore, aging needs an explanation from evolution, not from physics.

The first neo-Darwinst theory to be proposed (Medawar, 1952) was the idea of a “selection shadow”. The natural world is highly competitive, and no animals in the wild live long enough for their fitness to decline from age. This was a plausible idea when it was proposed, but field studies in the 1990s demonstrated that it is incorrect; indeed, many animals in the wild live long enough to die of old age. Half a century after Medawar, Ricklefs, Promislow, Bonduriansky, and Jones et al independently compiled evidence that, in the natural world, there is no selection shadow. 

The second neo-Darwinst theory (Williams, 1957) was that aging is a side-effect of genes for fertility. Fertility is so important to natural selection that fertility genes are selected even at the expense of deterioration and early death. There are many observed contradictions to this theory

• “Aging genes” have been discovered that have no fertility benefit. (For example)
• David Reznick and others have demonstrated natural genetic variants that increase fertility and longevity simultaneously
• Williams didn’t know about epigenetics in 1957. The idea that genes are routinely turned on when needed and off when they are not undermines Williams’s thesis that the body is “stuck with” genes when they are no longer useful.

The third neo-Darwinist theory was published by Tom Kirkwood (1977). He theorized that both bodily maintenance and reproduction require a lot of food energy; Aging results from the body’s need to compromise and short-change the repair budget. This is the most insupportable of the 3 theories. Kirkwood was probably unaware in 1977 that animals live longest when they are starved; but he certainly knew that females spend a lot more energy on reproduction than males, and they generally live longer. I don’t blame Kirkwood for publishing this idea as a young student, but I think it’s hard to explain why he has clung so fast to a failed theory 37 years on. 

The only solution to this dilemma is to abandon neo-Darwinism and adopt a perspective of multi-level selection (MLS). Neo-Darwinism asserts that all natural selection is individual selection, and that fitness of a community or a population is not a relevant concept. MLS asserts that fit individuals need cooperative communities and stable ecosystems, and all these levels can experience evolutionary selection. This is what I have argued since I entered the field 25 years ago. 

To avoid this deep re-thinking of evolutionary dynamics, many aging researchers re-cast the old entropic theory in terms of biological information. “Information” in general is the opposite of entropy, and it may be acquired freely in the form of food energy (animals) or sunlight (plants). But biological information is specific to the organism. Its source repository is in the DNA. Genetic information can be lost to somatic mutations. Epigenetic information can be lost when methylation and de-methylation enzymes experience occasional failures. This appears to be a one-way street — information lost cannot be recovered.

My view: This is true in theory, but in reality the body is well adapted to assure that its function does not suffer significantly from somatic mutations. [See Hayashi and Chapter 3 from my academic book]. DNA repair is robust. There are two copies of every chromosome, and there are molecular mechanisms that can not only repair breaks in DNA, but can respond to damaged DNA in consultation with the homologous area of the sister chromosome. Unlike genetic information, loss of epigenetic information need not be irreversible; the information remains rooted in the methylation dynamics that can recreate patterns lost to epigenetic drift. 

This is the context for the three papers this year which have proposed that the epigenetic changes underlying methylation clocks are stochastic.

The three papers

One

The first of these was [Meyer & Schumacher 2024]. It is a data-free proof-of-concept. The study uses simulated (computer-generated) methylation data to demonstrate how one would go about constructing a methylation clock based not on directed methylation changes but on loss of methylation information.

The reproducibility of accurate aging clocks has reinvigorated the debate on whether a programmed process underlies aging. Here we show that accumulating stochastic variation in purely simulated data is sufficient to build aging clocks.

So far, I have no problem with this. I agree that creating a clock from stochastic loss of information in the epigenome is feasible. See below, where I try to do it.,,,

Although our simulations may not explicitly rule out a programmed aging process, our results suggest that stochastically accumulating changes in any set of data that have a ground state at age zero are sufficient for generating aging clocks.

Yes, they have not ruled out programmed aging, and yes it is possible to create a clock algorithm from stochastic variation. But what is missing is the acknowledgement that all the most popular clocks were created by explicitly looking for sites that change methylation status consistently over a lifetime in a directed way. There is no reason to believe that the demonstration of feasibility has anything to do with the Horvath clocks, and the Horvath clocks, because of the way they were created, are evidence that methylation changes are directed, i.e., that aging is programmed. 

The authors proceed to build a clock around DNA sites that begin life either 100% methylated or unmethylated. In either case, random change can only occur in one direction. In these cases, it is difficult to distinguish random change from directed change. However, this is not what Horvath has done. Most of the sites in the original (2013) Horvath clock and subsequent clocks do not start out at 0 or 100%, so directed change looks far more likely than random change that happens to go in one direction only.

Under the kind of model that Meyer assumes, random methylation and random demethylation are equally likely, so over time the sites all trend toward 50% methylation. In real life, there is no reason to assume that methylation and demethylation are equally likely. In any case, the Horvath clocks contain partially methylated sites that trend toward the extremes with age as well as sites that trend toward 50%.

twO

Second is from the Harvard lab of Vadim Gladyshev. (Tarkhov et al 2024) is intricate in detail, and, IMO, difficult to follow. It is premised on the explicit assumption that aging is not programmed, and that any changes in methylation with age are either random drift or a response to damage (what I have called Type 2).  They cite Hayflick as a source for their understanding of where aging comes from, blithely ignoring the fact that entropic views of aging were discredited in the 19th century for sound reasons. 

Tarkhov’s thesis is that most epigenetic change with age is stochastic, while the residue is “co-regulated”. How does he define “co-regulated”, and how does he distinguish co-regulated from stochastic CpG’s?

As I read it, “co-regulated” sites are sites within a CpG island that turn on and off together. If the β of a given site is not well-correlated with βs of nearby sites, then change in this site are assumed to be stochastic.

My comment: To the extent that we understand methylation and epigenetics, a fully methylated CpG island turns off an adjacent gene, while a fully unmethylated CpG island turns it on. If this is the whole truth and nothing but the truth, then it would be irrational for the body to turn on some CpGs and not others, so we might regard CpG changes that are not “co-regulated” to be “stochastic”. But I wouldn’t assume that we understand the ways of biology well enough to build a theory around this premise. The cell may well have its reasons for methylating a particular site while leaving adjacent sites unmethylated.

I don’t understand the claim that “…clocks built on the co-regulated cluster of CpG sites may perform worse in the context of chronological age prediction but may be able to better capture the effects of longevity interventions.” If by “co-regulated” he means “Type 2”, then I have argued that Type 2 sites are a confounder for predicting benefits of longevity interventions.

“A more mechanistic understanding of epigenetic aging based on co-regulation may improve performance of epigenetic clocks in evaluating anti-aging interventions.” 

Three

The third and most deceptive of these is [Tong et al 2024]. They ask the question: how much of the computation in the most popular Horvath methylation clocks is attributable to directed methylation changes, and how much of it is stochastic? They conclude that most of it is stochastic. How do they arrive at this conclusion?

• They start with the sites that have already been chosen by Horvath because they change most consistently with age.
• For each of these, they note what direction the site changes with age, and how much methylation of that site changes with each passing year.
• They feed that information into an algorithm that “randomly” adds or subtracts methylation to each particular site at the appropriate rate. The process is “random” only in that the exact timing of each methylation addition or subtraction is random. But the probability has been pre-adjusted so that the average rate will match the measured rate according to the Horvath clock.
• Wonder of wonders! Somehow their “random” simulation manages to match the Horvath clock pretty well.

Am I dismissing this model too lightly? My point is only that the model is far from a random process. The title of the article and its stated conclusions are not warranted. 

A truly stochastic aging clock

The genome really does lose epigenetic focus with age, and it should be possible in theory to develop a clock algorithm on this basis. The way to do this would be to choose methylation sites that do not change, on average, from birth to death. There are many such sites. The clock would be based on the RMS average deviation (in either direction) of an individual’s methylation from “where it is supposed to be”.

I tried to do this last month. I have a small, older database in my computer, with methylation profiles of 278 individuals with an age range from 2 to 92. I spent just two days on the exercise, and the results suggested to me that the implementation of a stochastic methylation clock is not useful in practice. Here are the details, for those who are interested.

I searched a universe of 480,000 sites for those that met the following conditions:

• They had βs that stayed the same, on average, over the adult lifespan.
• Those average values were not close to 0 or to 1.
• The variance of the logistically-transformed βs among the oldest quarter of subjects was at least 100 times as large as the variance among the youngest quarter of subjects. There were 2300 such sites. (Logistic transform is defined as logit(β)=ln(β/(1-β)).)

From these 2300 sites, I constructed a clock. I reasoned that for each of the sites there was an average logit(β) where they “belonged”, and the the squared difference from this average represented drift which, by hypothesis, should increase with age. So my clock was based on the sum of squared differences of logit(β) from the average value.

I was surprised and disappointed that the correlation between this sum and chronological age was only 0.51, not high enough to be useful as a predictive clock. The RMS difference between predicted age and actual age was 17 years. 

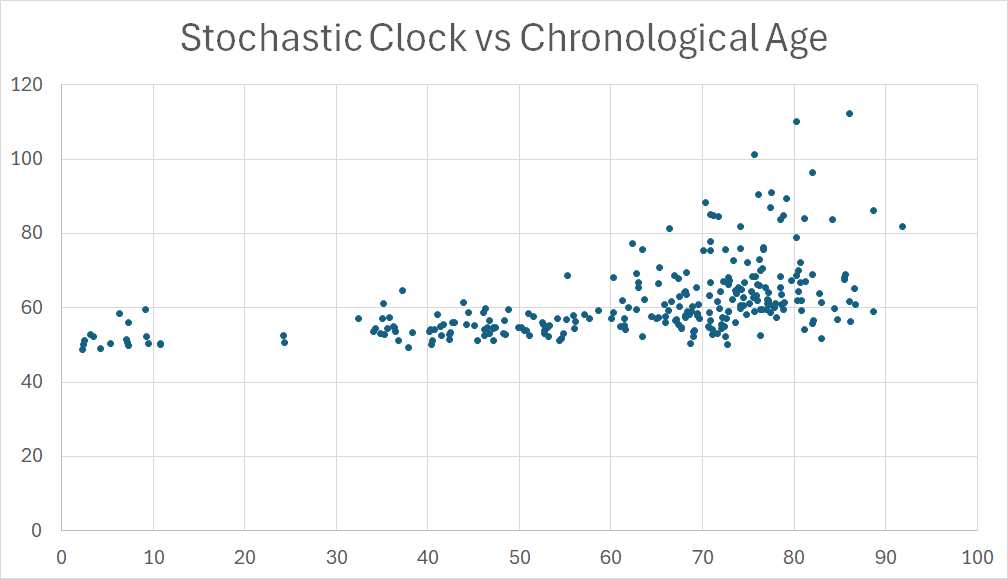
Before discarding the idea, I gave the method an extra benefit which was likely not to be sustainable when generalized. I redefined “ideal” for each logit(β) as the average of children. I calculated a squared departure from that average for each age, and calculated a correlation (for each CpG) of the squared departure with chronological age. The best correlation was only 0.25. I calculated, for each age, the sum of squared departures, now restricted to just the best 1,000 out of 23,000 sites. Since these 1,000 were chosen explicitly for their high performance, it is likely that some or most of them performed well just by chance; hence it is likely this methodology would not be sustainable when translated to a different data set. Nevertheless, the average of the “best 1,000” did not perform any better than the average over the full 23,000.

I concluded that this methodology does not appear to be promising.

The bottom line

Gene expression is among the most tightly controlled biochemical processes in any organism. It is natural to assume that changes in gene expression are under the body’s control, absent powerful evidence to the contrary.

Methylation clocks have always been designed around the CpG sites that change most reliably and consistently over time. While there is stochastic variation as well as directed change over a lifetime, the extant clocks are all based on the latter. 

The recent publications claiming that methylation clocks are based on stochastic change are ideologically driven. They have had to redefine “stochastic” to implement their models. The clocks that they construct and call “stochastic” have directed change built into their assumptions. 

I have done a preliminary exploration for a clock algorithm that is truly based on stochastic changes in methylation. I find that the results are far less accurate than clocks based on directed methylation changes.